Nhai kỹ sống chậm
Writer
Giải tích là một nhánh của toán học liên quan đến việc nghiên cứu tốc độ thay đổi. Trước khi giải tích được phát minh, tất cả toán học đều tĩnh: Nó chỉ có thể giúp tính toán các vật thể hoàn toàn đứng yên. Nhưng vũ trụ liên tục chuyển động và thay đổi. Không có vật thể nào - từ các ngôi sao trong không gian đến các hạt hạ nguyên tử hoặc tế bào trong cơ thể - luôn ở trạng thái nghỉ. Thật vậy, hầu như mọi thứ trong vũ trụ đều liên tục chuyển động. Giải tích đã giúp xác định cách các hạt, ngôi sao và vật chất thực sự chuyển động và thay đổi theo thời gian thực.
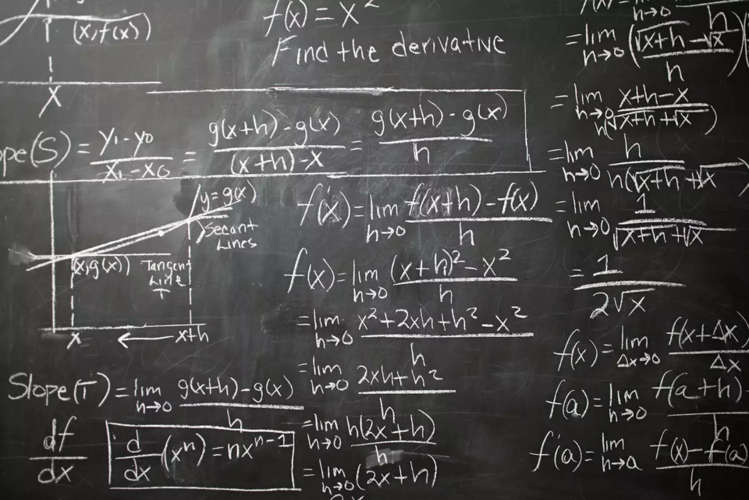
Giải tích được sử dụng trong nhiều lĩnh vực mà thông thường bạn không nghĩ sẽ sử dụng các khái niệm của nó. Trong số đó có vật lý, kỹ thuật, kinh tế, thống kê và y học. Giải tích cũng được sử dụng trong các lĩnh vực khác nhau như du hành vũ trụ, cũng như xác định cách thuốc tương tác với cơ thể và thậm chí là cách xây dựng các cấu trúc an toàn hơn. Bạn sẽ hiểu tại sao giải tích hữu ích trong nhiều lĩnh vực như vậy nếu bạn biết một chút về lịch sử của nó cũng như mục đích của nó và cách đo lường.
Những công cụ đó cho phép Newton, Leibniz và các nhà toán học khác sau này tính toán những thứ như độ dốc chính xác của một đường cong tại bất kỳ điểm nào. Câu chuyện Toán học giải thích tầm quan trọng của định lý cơ bản của Newton về phép tính:
Ngành này liên quan đến việc nghiên cứu tốc độ thay đổi của các hàm theo các biến của chúng, đặc biệt là thông qua việc sử dụng đạo hàm và vi phân. Đạo hàm là độ dốc của một đường thẳng trên đồ thị. Bạn tìm độ dốc của một đường thẳng bằng cách tính độ tăng trên đường chạy .
Ngược lại, phép tính tích phân tìm cách tìm ra số lượng mà tốc độ thay đổi được biết. Nhánh này tập trung vào các khái niệm như độ dốc của các đường tiếp tuyến và vận tốc. Trong khi phép tính vi phân tập trung vào bản thân đường cong, phép tính tích phân quan tâm đến không gian hoặc diện tích bên dưới đường cong. Phép tính tích phân được sử dụng để tính tổng kích thước hoặc giá trị, chẳng hạn như độ dài, diện tích và thể tích.
Giải tích đóng vai trò không thể thiếu trong sự phát triển của ngành hàng hải vào thế kỷ 17 và 18 vì nó cho phép các thủy thủ sử dụng vị trí của mặt trăng để xác định chính xác giờ địa phương. Để lập biểu đồ vị trí của họ trên biển, các nhà hàng hải cần có khả năng đo cả thời gian và góc một cách chính xác. Trước khi giải tích phát triển, các nhà hàng hải và thuyền trưởng không thể làm được cả hai.
Giải tích - cả đạo hàm và tích phân - đã giúp cải thiện sự hiểu biết về khái niệm quan trọng này liên quan đến đường cong của Trái Đất, khoảng cách mà tàu thuyền phải di chuyển quanh một đường cong để đến một địa điểm cụ thể, và thậm chí cả sự liên kết của Trái Đất, biển cả và tàu thuyền liên quan đến các vì sao.
Ví dụ, trong vật lý, phép tính được sử dụng để giúp xác định, giải thích và tính toán chuyển động, điện, nhiệt, ánh sáng, sóng hài, âm học, thiên văn học và động lực học. Thuyết tương đối của Einstein dựa trên phép tính, một lĩnh vực toán học cũng giúp các nhà kinh tế dự đoán lợi nhuận mà một công ty hoặc ngành công nghiệp có thể tạo ra. Và trong đóng tàu , phép tính đã được sử dụng trong nhiều năm để xác định cả đường cong của thân tàu (sử dụng phép tính vi phân), cũng như diện tích bên dưới thân tàu (sử dụng phép tính tích phân), và thậm chí trong thiết kế chung của tàu.
Ngoài ra, phép tính còn được sử dụng để kiểm tra câu trả lời cho nhiều môn toán khác nhau như thống kê, hình học giải tích và đại số.
Các nhà kinh tế sử dụng phép tính để xác định độ co giãn giá của cầu . Họ gọi đường cung cầu luôn thay đổi là "co giãn" và các hành động của đường cong là "độ co giãn". Để tính toán một phép đo chính xác về độ co giãn tại một điểm cụ thể trên đường cung hoặc đường cầu, bạn cần nghĩ về những thay đổi vô cùng nhỏ về giá và kết quả là kết hợp các đạo hàm toán học vào các công thức độ co giãn của bạn. Phép tính cho phép bạn xác định các điểm cụ thể trên đường cung cầu luôn thay đổi đó.
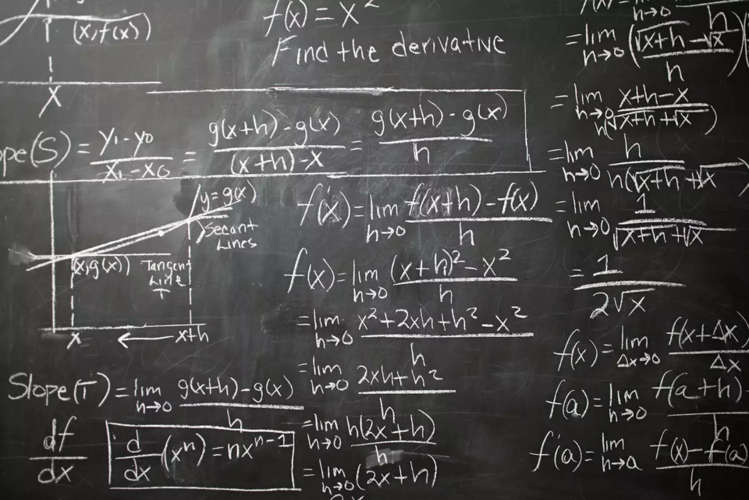
Giải tích được sử dụng trong nhiều lĩnh vực mà thông thường bạn không nghĩ sẽ sử dụng các khái niệm của nó. Trong số đó có vật lý, kỹ thuật, kinh tế, thống kê và y học. Giải tích cũng được sử dụng trong các lĩnh vực khác nhau như du hành vũ trụ, cũng như xác định cách thuốc tương tác với cơ thể và thậm chí là cách xây dựng các cấu trúc an toàn hơn. Bạn sẽ hiểu tại sao giải tích hữu ích trong nhiều lĩnh vực như vậy nếu bạn biết một chút về lịch sử của nó cũng như mục đích của nó và cách đo lường.
Ai là người phát minh ra phép tính vi phân?
Giải tích được phát triển vào nửa sau thế kỷ 17 bởi hai nhà toán học, Gottfried Leibniz và Isaac Newton. Newton đầu tiên phát triển phép tính và áp dụng trực tiếp vào việc hiểu các hệ thống vật lý. Độc lập với Leibniz, ông đã phát triển các ký hiệu được sử dụng trong phép tính. Nói một cách đơn giản, trong khi toán học cơ bản sử dụng các phép toán như cộng, trừ, nhân và chia (+, -, x và ÷), phép tính sử dụng các phép toán sử dụng hàm và tích phân để tính tốc độ thay đổi.Những công cụ đó cho phép Newton, Leibniz và các nhà toán học khác sau này tính toán những thứ như độ dốc chính xác của một đường cong tại bất kỳ điểm nào. Câu chuyện Toán học giải thích tầm quan trọng của định lý cơ bản của Newton về phép tính:
Bằng cách sử dụng phép tính, các nhà khoa học, nhà thiên văn học, nhà vật lý, nhà toán học và nhà hóa học giờ đây có thể lập biểu đồ quỹ đạo của các hành tinh và ngôi sao, cũng như đường đi của các electron và proton ở cấp độ nguyên tử.
Phép tính vi phân và tích phân
Có hai nhánh của phép tính: phép tính vi phân và tích phân. "Phép tính vi phân nghiên cứu phép tính đạo hàm và tích phân nghiên cứu...tích phân", Viện Công nghệ Massachusetts lưu ý. Nhưng còn nhiều hơn thế nữa. Phép tính vi phân xác định tốc độ thay đổi của một lượng. Nó kiểm tra tốc độ thay đổi của độ dốc và đường cong.Ngành này liên quan đến việc nghiên cứu tốc độ thay đổi của các hàm theo các biến của chúng, đặc biệt là thông qua việc sử dụng đạo hàm và vi phân. Đạo hàm là độ dốc của một đường thẳng trên đồ thị. Bạn tìm độ dốc của một đường thẳng bằng cách tính độ tăng trên đường chạy .
Ngược lại, phép tính tích phân tìm cách tìm ra số lượng mà tốc độ thay đổi được biết. Nhánh này tập trung vào các khái niệm như độ dốc của các đường tiếp tuyến và vận tốc. Trong khi phép tính vi phân tập trung vào bản thân đường cong, phép tính tích phân quan tâm đến không gian hoặc diện tích bên dưới đường cong. Phép tính tích phân được sử dụng để tính tổng kích thước hoặc giá trị, chẳng hạn như độ dài, diện tích và thể tích.
Giải tích đóng vai trò không thể thiếu trong sự phát triển của ngành hàng hải vào thế kỷ 17 và 18 vì nó cho phép các thủy thủ sử dụng vị trí của mặt trăng để xác định chính xác giờ địa phương. Để lập biểu đồ vị trí của họ trên biển, các nhà hàng hải cần có khả năng đo cả thời gian và góc một cách chính xác. Trước khi giải tích phát triển, các nhà hàng hải và thuyền trưởng không thể làm được cả hai.
Giải tích - cả đạo hàm và tích phân - đã giúp cải thiện sự hiểu biết về khái niệm quan trọng này liên quan đến đường cong của Trái Đất, khoảng cách mà tàu thuyền phải di chuyển quanh một đường cong để đến một địa điểm cụ thể, và thậm chí cả sự liên kết của Trái Đất, biển cả và tàu thuyền liên quan đến các vì sao.
Ứng dụng thực tế
Giải tích có nhiều ứng dụng thực tế trong cuộc sống thực. Một số khái niệm sử dụng giải tích bao gồm chuyển động, điện, nhiệt, ánh sáng, sóng hài, âm học và thiên văn học. Giải tích được sử dụng trong địa lý, thị giác máy tính (chẳng hạn như để lái xe tự động), nhiếp ảnh, trí tuệ nhân tạo, robot, trò chơi điện tử và thậm chí cả phim ảnh. Giải tích cũng được sử dụng để tính tốc độ phân rã phóng xạ trong hóa học và thậm chí để dự đoán tỷ lệ sinh và tử, cũng như trong nghiên cứu về trọng lực và chuyển động của hành tinh, dòng chảy chất lỏng, thiết kế tàu, đường cong hình học và kỹ thuật cầu.Ví dụ, trong vật lý, phép tính được sử dụng để giúp xác định, giải thích và tính toán chuyển động, điện, nhiệt, ánh sáng, sóng hài, âm học, thiên văn học và động lực học. Thuyết tương đối của Einstein dựa trên phép tính, một lĩnh vực toán học cũng giúp các nhà kinh tế dự đoán lợi nhuận mà một công ty hoặc ngành công nghiệp có thể tạo ra. Và trong đóng tàu , phép tính đã được sử dụng trong nhiều năm để xác định cả đường cong của thân tàu (sử dụng phép tính vi phân), cũng như diện tích bên dưới thân tàu (sử dụng phép tính tích phân), và thậm chí trong thiết kế chung của tàu.
Ngoài ra, phép tính còn được sử dụng để kiểm tra câu trả lời cho nhiều môn toán khác nhau như thống kê, hình học giải tích và đại số.
Giải tích trong kinh tế
Các nhà kinh tế sử dụng phép tính để dự đoán cung, cầu và lợi nhuận tiềm năng tối đa. Xét cho cùng, cung và cầu về cơ bản được biểu diễn trên một đường cong - và một đường cong luôn thay đổi.Các nhà kinh tế sử dụng phép tính để xác định độ co giãn giá của cầu . Họ gọi đường cung cầu luôn thay đổi là "co giãn" và các hành động của đường cong là "độ co giãn". Để tính toán một phép đo chính xác về độ co giãn tại một điểm cụ thể trên đường cung hoặc đường cầu, bạn cần nghĩ về những thay đổi vô cùng nhỏ về giá và kết quả là kết hợp các đạo hàm toán học vào các công thức độ co giãn của bạn. Phép tính cho phép bạn xác định các điểm cụ thể trên đường cung cầu luôn thay đổi đó.
