Trường Sơn
Writer
DeepSeek đã lặng lẽ đăng tải một mô hình mới trên Hugging Face: DeepSeek-Math-V2. Đúng như tên gọi, đây là một mô hình trong thuật ngữ toán học. Phiên bản trước là DeepSeek-Math-7b đã được phát hành hơn một năm trước. Khi đó, model này chỉ sử dụng thông số 7B để đạt được mức hiệu suất tương tự như GPT-4 và Gemini-Ultra. GRPO cũng được giới thiệu lần đầu tiên, cải thiện đáng kể khả năng suy luận toán học.
Sau một năm rưỡi, DeepSeek-Math-V2 dựa trên DeepSeek-V3.2-Exp-Base này đã mang lại những bất ngờ gì?
DeepSeek cho biết nó vượt trội hơn Gemini DeepThink, đạt được mức huy chương vàng Toán quốc tế IMO.

Mặc dù cách tiếp cận này cho phép các mô hình suy luận đạt đến mức cao hơn và thậm chí bão hòa trên các điểm chuẩn như AIME và HMMT, nhưng DeepSeek cho biết nó không giải quyết được vấn đề cốt lõi: câu trả lời đúng không đảm bảo rằng quá trình suy luận là đúng. Ngoài ra, nhiều nhiệm vụ toán học, chẳng hạn như chứng minh định lý, yêu cầu suy ra từng bước nghiêm ngặt thay vì chỉ câu trả lời số, khiến các phương pháp khen thưởng dựa trên câu trả lời cuối cùng không thể áp dụng được.
Để vượt qua giới hạn của lý luận sâu sắc, DeepSeek tin rằng cần phải xác nhận tính toàn diện và chặt chẽ của lý luận toán học.
"Tự xác nhận đặc biệt quan trọng khi mở rộng quy mô tính toán trong thử nghiệm, đặc biệt là đối với các vấn đề mở không có giải pháp được biết đến", họ lưu ý.
Để đạt được lý luận toán học có thể tự xác minh, DeepSeek đã nghiên cứu cách đào tạo trình xác thực chứng minh định lý dựa trên LLM chính xác và đáng tin cậy. Sau đó, họ sử dụng trình xác thực này như một mô hình phần thưởng để đào tạo trình tạo chứng minh và khuyến khích trình tạo tìm và giải quyết các vấn đề trong bằng chứng của riêng nó càng nhiều càng tốt trước khi hoàn thiện chứng minh.
Để duy trì khoảng cách xác thực thế hệ khi khả năng của trình tạo tăng lên, DeepSeek đề xuất mở rộng sức mạnh tính toán xác thực để tự động gắn nhãn các bằng chứng mới khó xác minh, từ đó tạo dữ liệu đào tạo để cải thiện hơn nữa hiệu suất của trình xác thực.
Nói tóm lại, mục tiêu cốt lõi của bài báo của DeepSeek không chỉ là làm cho AI đúng, mà còn cho phép AI "không chỉ làm điều đó mà còn tự kiểm tra nó và thậm chí thành thật thừa nhận nó đã làm điều gì đó sai trái".
Để đạt được điều này, họ đã thiết kế một hệ thống gồm ba vai trò chính, có thể được hiểu bằng phép so sánh học sinh-giáo viên-giám sát:
Đầu tiên, đào tạo "Xác minh bằng chứng" đủ điều kiện.
Trước đây, các mô hình toán học AI được đào tạo chỉ dựa trên câu trả lời cuối cùng có đúng hay không. Tuy nhiên, trong các câu hỏi chứng minh toán học nâng cao (chẳng hạn như Olympic Toán học), sự nghiêm ngặt của quy trình quan trọng hơn câu trả lời. Do đó, nhóm DeepSeek đầu tiên đã đào tạo một người xác minh đặc biệt, đó là "giáo viên chấm điểm". Người thầy này không chỉ đánh dấu và vượt qua, mà còn học cách chia quá trình chứng minh thành ba cấp độ như một chuyên gia con người:
Tiếp theo, chỉ định cho giáo viên một "Xác minh tổng hợp".
DeepSeek tìm thấy một vấn đề: giáo viên chấm điểm đôi khi bị trừ điểm bừa bãi và nó có thể cho điểm thấp, nhưng sai lầm được chỉ ra không thực sự tồn tại (tức là ảo giác).
Để giải quyết vấn đề này, họ đã giới thiệu một cơ chế xác minh meta, tương đương với việc chỉ định một "người giám sát" cho giáo viên. Nhiệm vụ của người giám sát không phải là nhìn vào đề thi, mà là kiểm tra xem những "nhận xét" do giáo viên viết có hợp lý hay không. Điều này cho phép xác nhận kép: người giám sát kiểm tra xem những sai lầm do giáo viên chỉ ra có thật hay không và liệu suy luận có hợp lý hay không. Về hiệu quả, bằng cách đào tạo mô hình vừa là giáo viên vừa là người giám sát, độ chính xác và độ tin cậy của bằng chứng đánh giá AI đã được cải thiện đáng kể.
Sau đó, phát triển những học sinh sẽ "tuyên bố" (Proof Generation with Self-Verification).
Với một hệ thống chấm điểm tốt, bước tiếp theo là đào tạo các "học sinh" (generators) làm các câu hỏi. Đây là một sự đổi mới rất quan trọng: phần thưởng trung thực. Nói cách khác, nó không chỉ thực hiện vấn đề mà còn tự đánh giá: sau khi mô hình xuất ra quá trình giải quyết vấn đề, nó phải ngay lập tức thực hiện "tự đánh giá" và tự chấm điểm (0, 0,5 hoặc 1).
Nó thưởng cho sự trung thực:
Cuối cùng, tạo thành một vòng lặp khép kín tự động (Synergy).
Các chuyên gia con người không thể viết điểm chi tiết từng bước cho hàng nghìn Olympic Toán học, vì vậy DeepSeek đã thiết kế một quy trình tự động cho phép hệ thống tự phát triển:
Cuối cùng, họ đã có được mô hình DeepSeekMath-V2, thể hiện khả năng chứng minh định lý mạnh mẽ: nó đạt được kết quả cấp vàng tại IMO 2025 và CMO 2024, đồng thời đạt được số điểm gần như hoàn hảo là 118/120 trong các tính toán thử nghiệm mở rộng vào năm 2024.

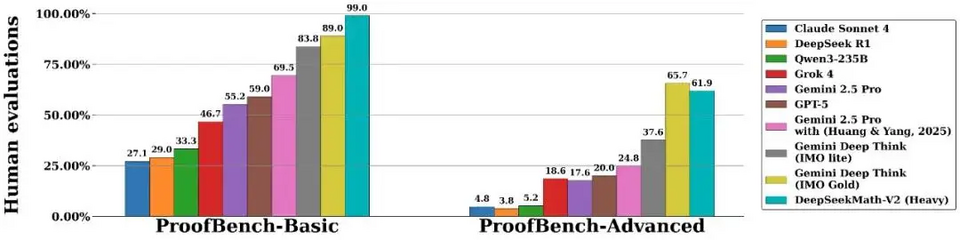
Biểu đồ dưới đây cho thấy hiệu suất của DeepSeekMath-V2 trên điểm chuẩn IMO-ProofBench (là một tập hợp con của IMO Bench với 60 câu hỏi chứng minh) và có thể thấy rằng DeepSeekMath-V2 không chỉ vượt trội hơn các mô hình khác trong điểm chuẩn Cơ bản, mà thậm chí còn đạt được số điểm cao ấn tượng gần 99%. Và trên tập con Nâng cao khó hơn, DeepSeekMath-V2 kém hơn một chút so với Gemini Deep Think (IMO Gold).
"Mặc dù vẫn còn rất nhiều việc phải làm, nhưng những kết quả này cho thấy rằng lý luận toán học có thể tự xác minh là một hướng nghiên cứu khả thi có tiềm năng thúc đẩy sự phát triển của các hệ thống AI toán học mạnh mẽ hơn", DeepSeek nói.
Khung lý luận toán học tự xác thực này có thể nói là phá vỡ những hạn chế của học tăng cường truyền thống (RL), cho phép mô hình tập trung vào sự chặt chẽ của quá trình suy luận thay vì dựa vào tính đúng đắn của câu trả lời cuối cùng như phần thưởng duy nhất. Ngoài ra, sức mạnh tổng hợp giữa trình xác thực-trình tạo trong DeepSeekMath-V2 mang lại khả năng suy luận toán học toàn diện và nghiêm ngặt, giảm đáng kể ảo giác mô hình lớn.
Trong bài báo, DeepSeek giới thiệu thêm các chi tiết kỹ thuật mà sinh viên quan tâm có thể đọc kỹ. #DeepSeekMath
Sau một năm rưỡi, DeepSeek-Math-V2 dựa trên DeepSeek-V3.2-Exp-Base này đã mang lại những bất ngờ gì?
DeepSeek cho biết nó vượt trội hơn Gemini DeepThink, đạt được mức huy chương vàng Toán quốc tế IMO.

- Tiêu đề bài báo: DeepSeekMath-V2: Hướng tới lý luận toán học có thể tự kiểm chứng
- Địa chỉ mô hình: https://huggingface.co/deepseek-ai/DeepSeek-Math-V2
- Địa chỉ bài báo: https://github.com/deepseek-ai/DeepSeek-Math-V2/blob/main/DeepSeekMath_V2.pdf
- Tác giả chính: Shao Zhihong, Yuxiang Luo, Chengda Lu, ZZ Ren
Mặc dù cách tiếp cận này cho phép các mô hình suy luận đạt đến mức cao hơn và thậm chí bão hòa trên các điểm chuẩn như AIME và HMMT, nhưng DeepSeek cho biết nó không giải quyết được vấn đề cốt lõi: câu trả lời đúng không đảm bảo rằng quá trình suy luận là đúng. Ngoài ra, nhiều nhiệm vụ toán học, chẳng hạn như chứng minh định lý, yêu cầu suy ra từng bước nghiêm ngặt thay vì chỉ câu trả lời số, khiến các phương pháp khen thưởng dựa trên câu trả lời cuối cùng không thể áp dụng được.
Để vượt qua giới hạn của lý luận sâu sắc, DeepSeek tin rằng cần phải xác nhận tính toàn diện và chặt chẽ của lý luận toán học.
"Tự xác nhận đặc biệt quan trọng khi mở rộng quy mô tính toán trong thử nghiệm, đặc biệt là đối với các vấn đề mở không có giải pháp được biết đến", họ lưu ý.
Để đạt được lý luận toán học có thể tự xác minh, DeepSeek đã nghiên cứu cách đào tạo trình xác thực chứng minh định lý dựa trên LLM chính xác và đáng tin cậy. Sau đó, họ sử dụng trình xác thực này như một mô hình phần thưởng để đào tạo trình tạo chứng minh và khuyến khích trình tạo tìm và giải quyết các vấn đề trong bằng chứng của riêng nó càng nhiều càng tốt trước khi hoàn thiện chứng minh.
Để duy trì khoảng cách xác thực thế hệ khi khả năng của trình tạo tăng lên, DeepSeek đề xuất mở rộng sức mạnh tính toán xác thực để tự động gắn nhãn các bằng chứng mới khó xác minh, từ đó tạo dữ liệu đào tạo để cải thiện hơn nữa hiệu suất của trình xác thực.
Nói tóm lại, mục tiêu cốt lõi của bài báo của DeepSeek không chỉ là làm cho AI đúng, mà còn cho phép AI "không chỉ làm điều đó mà còn tự kiểm tra nó và thậm chí thành thật thừa nhận nó đã làm điều gì đó sai trái".
Để đạt được điều này, họ đã thiết kế một hệ thống gồm ba vai trò chính, có thể được hiểu bằng phép so sánh học sinh-giáo viên-giám sát:
Đầu tiên, đào tạo "Xác minh bằng chứng" đủ điều kiện.
Trước đây, các mô hình toán học AI được đào tạo chỉ dựa trên câu trả lời cuối cùng có đúng hay không. Tuy nhiên, trong các câu hỏi chứng minh toán học nâng cao (chẳng hạn như Olympic Toán học), sự nghiêm ngặt của quy trình quan trọng hơn câu trả lời. Do đó, nhóm DeepSeek đầu tiên đã đào tạo một người xác minh đặc biệt, đó là "giáo viên chấm điểm". Người thầy này không chỉ đánh dấu và vượt qua, mà còn học cách chia quá trình chứng minh thành ba cấp độ như một chuyên gia con người:
- 1 điểm: hoàn hảo, logic.
- 0,5 điểm: Nói chung là đúng, nhưng có những sai sót nhỏ hoặc thiếu chi tiết.
- 0 điểm: Có lỗi logic cơ bản hoặc vắng mặt nghiêm trọng.
Tiếp theo, chỉ định cho giáo viên một "Xác minh tổng hợp".
DeepSeek tìm thấy một vấn đề: giáo viên chấm điểm đôi khi bị trừ điểm bừa bãi và nó có thể cho điểm thấp, nhưng sai lầm được chỉ ra không thực sự tồn tại (tức là ảo giác).
Để giải quyết vấn đề này, họ đã giới thiệu một cơ chế xác minh meta, tương đương với việc chỉ định một "người giám sát" cho giáo viên. Nhiệm vụ của người giám sát không phải là nhìn vào đề thi, mà là kiểm tra xem những "nhận xét" do giáo viên viết có hợp lý hay không. Điều này cho phép xác nhận kép: người giám sát kiểm tra xem những sai lầm do giáo viên chỉ ra có thật hay không và liệu suy luận có hợp lý hay không. Về hiệu quả, bằng cách đào tạo mô hình vừa là giáo viên vừa là người giám sát, độ chính xác và độ tin cậy của bằng chứng đánh giá AI đã được cải thiện đáng kể.
Sau đó, phát triển những học sinh sẽ "tuyên bố" (Proof Generation with Self-Verification).
Với một hệ thống chấm điểm tốt, bước tiếp theo là đào tạo các "học sinh" (generators) làm các câu hỏi. Đây là một sự đổi mới rất quan trọng: phần thưởng trung thực. Nói cách khác, nó không chỉ thực hiện vấn đề mà còn tự đánh giá: sau khi mô hình xuất ra quá trình giải quyết vấn đề, nó phải ngay lập tức thực hiện "tự đánh giá" và tự chấm điểm (0, 0,5 hoặc 1).
Nó thưởng cho sự trung thực:
- Nếu mô hình làm điều gì đó sai, nhưng nó thành thật chỉ ra những sai lầm của mình trong quá trình tự đánh giá, nó sẽ được khen thưởng.
- Ngược lại, nếu nó làm điều gì đó sai nhưng khăng khăng rằng nó đúng (sự tự tin mù quáng), hoặc cố gắng "vượt qua", nó sẽ bị trừng phạt (không có phần thưởng cao).
Cuối cùng, tạo thành một vòng lặp khép kín tự động (Synergy).
Các chuyên gia con người không thể viết điểm chi tiết từng bước cho hàng nghìn Olympic Toán học, vì vậy DeepSeek đã thiết kế một quy trình tự động cho phép hệ thống tự phát triển:
- Thế hệ đại chúng: Hãy để "sinh viên" tạo ra nhiều giải pháp cho cùng một vấn đề.
- Bỏ phiếu tập thể: Yêu cầu "giáo viên" đánh giá các giải pháp này nhiều lần. Nếu hầu hết các đánh giá coi một giải pháp là có vấn đề, thì nó được coi là có vấn đề; Nếu không tìm thấy lỗ hổng nào thì sẽ được đánh giá là đúng.
- Bằng cách này, hệ thống tự động sàng lọc những câu hỏi khó đánh giá hoặc khó trả lời đúng, biến chúng thành tài liệu giảng dạy mới và đào tạo lại "giáo viên" và "học sinh". Bằng cách này, khi khả năng giải quyết vấn đề của "học sinh" trở nên mạnh mẽ hơn, tầm nhìn của "giáo viên" ngày càng trở nên xấu xa.
Cuối cùng, họ đã có được mô hình DeepSeekMath-V2, thể hiện khả năng chứng minh định lý mạnh mẽ: nó đạt được kết quả cấp vàng tại IMO 2025 và CMO 2024, đồng thời đạt được số điểm gần như hoàn hảo là 118/120 trong các tính toán thử nghiệm mở rộng vào năm 2024.

Biểu đồ dưới đây cho thấy hiệu suất của DeepSeekMath-V2 trên điểm chuẩn IMO-ProofBench (là một tập hợp con của IMO Bench với 60 câu hỏi chứng minh) và có thể thấy rằng DeepSeekMath-V2 không chỉ vượt trội hơn các mô hình khác trong điểm chuẩn Cơ bản, mà thậm chí còn đạt được số điểm cao ấn tượng gần 99%. Và trên tập con Nâng cao khó hơn, DeepSeekMath-V2 kém hơn một chút so với Gemini Deep Think (IMO Gold).

"Mặc dù vẫn còn rất nhiều việc phải làm, nhưng những kết quả này cho thấy rằng lý luận toán học có thể tự xác minh là một hướng nghiên cứu khả thi có tiềm năng thúc đẩy sự phát triển của các hệ thống AI toán học mạnh mẽ hơn", DeepSeek nói.
Khung lý luận toán học tự xác thực này có thể nói là phá vỡ những hạn chế của học tăng cường truyền thống (RL), cho phép mô hình tập trung vào sự chặt chẽ của quá trình suy luận thay vì dựa vào tính đúng đắn của câu trả lời cuối cùng như phần thưởng duy nhất. Ngoài ra, sức mạnh tổng hợp giữa trình xác thực-trình tạo trong DeepSeekMath-V2 mang lại khả năng suy luận toán học toàn diện và nghiêm ngặt, giảm đáng kể ảo giác mô hình lớn.
Trong bài báo, DeepSeek giới thiệu thêm các chi tiết kỹ thuật mà sinh viên quan tâm có thể đọc kỹ. #DeepSeekMath