Lizzie
Writer
Trực giác là một công cụ mạnh mẽ trong đời sống thường ngày, nhưng khi chạm đến xác suất – đặc biệt là xác suất có điều kiện – nó thường phản bội chúng ta. Có những bài toán nghe thì đơn giản, nhưng khi đào sâu vào lại cho thấy rằng cảm giác "rõ ràng đúng" ban đầu hoàn toàn có thể sai. Một trong số những ví dụ tiêu biểu là câu đố “ba hộp bóng” nổi tiếng trên Reddit, tưởng như chỉ là trò đố mẹo nhẹ nhàng, nhưng thực tế đã đánh lừa rất nhiều người.
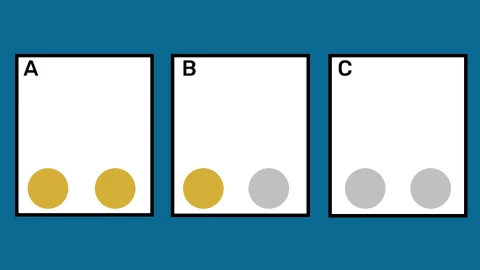
Bài toán được đặt ra như sau: có ba cái hộp, mỗi hộp chứa hai quả bóng. Một hộp có hai quả bóng vàng, một hộp có hai quả bóng bạc, và hộp còn lại có một quả bóng vàng và một quả bóng bạc. Bạn chọn ngẫu nhiên một hộp, thò tay vào rút một quả bóng và đó là một quả bóng vàng. Không được nhìn vào trong hộp. Câu hỏi là: xác suất quả bóng tiếp theo bạn rút ra từ cùng hộp đó là bóng bạc là bao nhiêu?
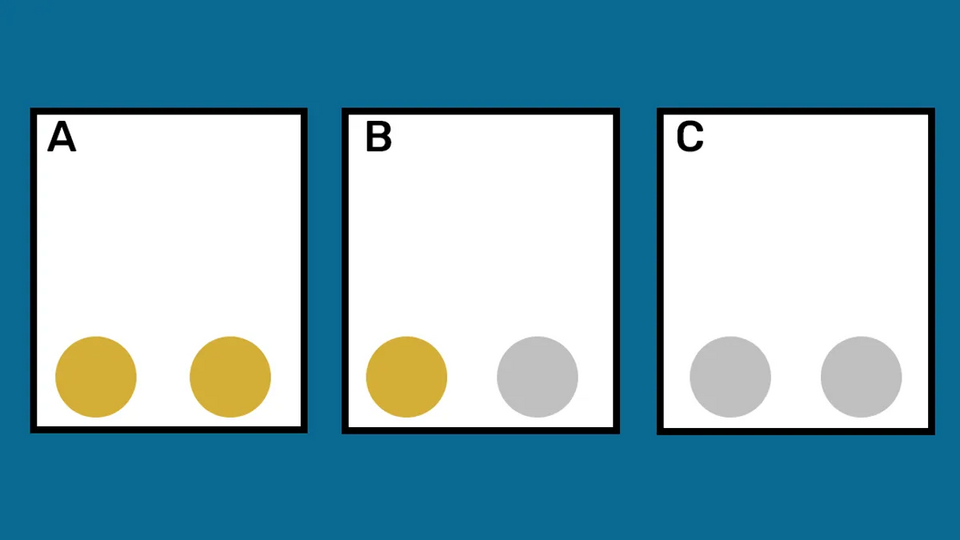
Phần lớn người tham gia sẽ trả lời 50%. Lý do nghe có vẻ rất hợp lý: vì bạn đã rút được một quả bóng vàng, tức là bạn không ở hộp chứa hai bóng bạc. Như vậy, khả năng bạn đang ở một trong hai hộp còn lại, hộp hai bóng vàng hoặc hộp một vàng một bạc, là ngang nhau. Một trong hai hộp còn lại một quả vàng, một thì còn một quả bạc, nên xác suất rút bóng bạc còn lại là 1/2. Có vẻ thuyết phục, nhưng lại sai.
Vấn đề nằm ở chỗ: xác suất không chỉ phụ thuộc vào những khả năng bạn đang nghĩ đến, mà còn phụ thuộc vào cách những khả năng đó có thể xảy ra. Nếu bạn nhìn kỹ hơn, có ba quả bóng vàng tồn tại trong tổng thể: hai quả ở hộp hai bóng vàng, một quả ở hộp vàng-bạc. Nếu bạn đã rút được một quả bóng vàng, thì bạn có thể đang ở trong ba tình huống: đã lấy một trong hai quả vàng từ hộp toàn vàng (hai khả năng), hoặc lấy quả vàng duy nhất từ hộp vàng-bạc (một khả năng). Như vậy, xác suất bạn đang ở hộp vàng-bạc thực ra chỉ là 1/3, còn 2/3 khả năng là bạn đang ở hộp toàn vàng – nơi quả bóng tiếp theo cũng sẽ là vàng. Vậy xác suất rút bóng bạc tiếp theo chỉ là 33%.
Tại sao trực giác lại lạc lối? Bởi vì nó bỏ qua cấu trúc xác suất ẩn phía sau dữ kiện đã biết. Nó chỉ nhìn bề mặt: có hai hộp hợp lý, mỗi hộp có một khả năng đúng, nên suy ra 50%. Nhưng khi bạn hiểu rõ rằng khả năng lấy ra một quả bóng vàng từ hộp toàn vàng là gấp đôi so với hộp vàng-bạc, thì bạn mới thấy trực giác ban đầu đã đơn giản hóa vấn đề một cách sai lầm.
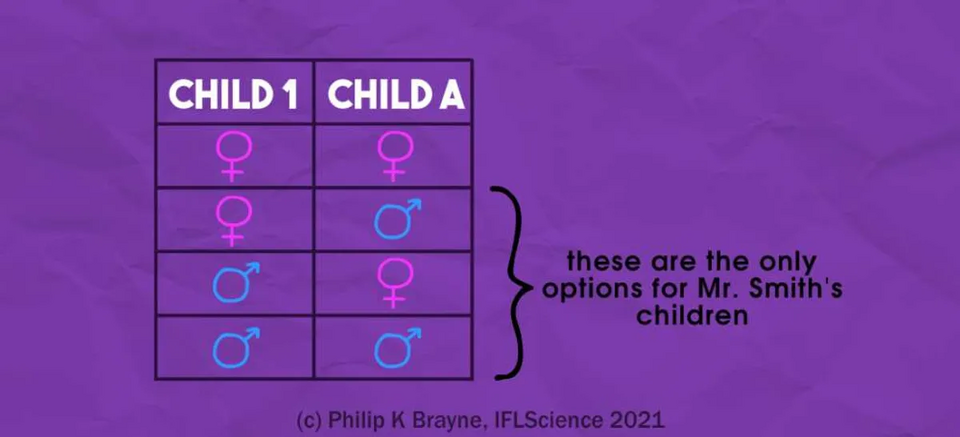
Trường hợp thứ hai, bài toán "hai con của ông Smith", còn nổi tiếng hơn về khả năng đánh lừa người thông minh. Câu hỏi là: "Ông Smith có hai người con. Một trong hai là con trai. Vậy xác suất cả hai đều là con trai là bao nhiêu?" Và lần nữa, rất nhiều người trả lời 50%, vì họ nghĩ đơn giản rằng nếu một đứa là trai, đứa còn lại có thể là trai hoặc gái – nên mỗi khả năng có 50%.
Nhưng sự thật cũng giống như câu chuyện về ba hộp bóng. Khi bạn liệt kê tất cả các khả năng có thể xảy ra với hai đứa trẻ (giả sử không phân biệt thứ tự sinh), bạn có: trai-trai, trai-gái, gái-trai và gái-gái. Nhưng đề bài đã nói rõ “một trong hai là trai”, nên bạn loại bỏ trường hợp gái-gái. Còn lại ba khả năng hợp lệ. Trong số đó, chỉ có một là cả hai cùng là trai. Vì vậy, xác suất đúng phải là 1/3, tức 33%.
Những ví dụ như thế này không chỉ là trò đùa toán học – chúng cho thấy một thực tế sâu sắc: xác suất không phải là cảm giác. Nó không hoạt động dựa trên "có vẻ công bằng" hay "một nửa là hợp lý". Nó hoạt động dựa trên tập hợp đầy đủ các khả năng, và cách các điều kiện đã biết làm thay đổi phân bố các khả năng đó.
Ngay cả những nhà toán học huyền thoại cũng từng lạc lối trong mê cung của xác suất có điều kiện. Paul Erdős, một trong những tên tuổi lớn nhất của thế kỷ 20, khi được nghe bài toán Monty Hall – một câu đố xác suất kinh điển khác – cũng nhất mực cho rằng "việc mở một cánh cửa không thay đổi gì cả". Dù người đối thoại với ông đã giải thích bằng công thức Bayes, cây quyết định, và dẫn chứng cụ thể, Erdős vẫn không bị thuyết phục. Một người có đầu óc toán học siêu việt, nhưng vẫn có thể bị trực giác dẫn sai đường.
Xác suất có điều kiện không tuân theo logic đơn giản hay công bằng cảm tính. Nó đòi hỏi sự cẩn trọng trong phân tích và một sự cảnh giác nhất định với trực giác. Đôi khi, để hiểu điều gì là “rõ ràng”, ta phải nghi ngờ chính những gì tưởng là hiển nhiên nhất.
Bài toán được đặt ra như sau: có ba cái hộp, mỗi hộp chứa hai quả bóng. Một hộp có hai quả bóng vàng, một hộp có hai quả bóng bạc, và hộp còn lại có một quả bóng vàng và một quả bóng bạc. Bạn chọn ngẫu nhiên một hộp, thò tay vào rút một quả bóng và đó là một quả bóng vàng. Không được nhìn vào trong hộp. Câu hỏi là: xác suất quả bóng tiếp theo bạn rút ra từ cùng hộp đó là bóng bạc là bao nhiêu?

Phần lớn người tham gia sẽ trả lời 50%. Lý do nghe có vẻ rất hợp lý: vì bạn đã rút được một quả bóng vàng, tức là bạn không ở hộp chứa hai bóng bạc. Như vậy, khả năng bạn đang ở một trong hai hộp còn lại, hộp hai bóng vàng hoặc hộp một vàng một bạc, là ngang nhau. Một trong hai hộp còn lại một quả vàng, một thì còn một quả bạc, nên xác suất rút bóng bạc còn lại là 1/2. Có vẻ thuyết phục, nhưng lại sai.
Vấn đề nằm ở chỗ: xác suất không chỉ phụ thuộc vào những khả năng bạn đang nghĩ đến, mà còn phụ thuộc vào cách những khả năng đó có thể xảy ra. Nếu bạn nhìn kỹ hơn, có ba quả bóng vàng tồn tại trong tổng thể: hai quả ở hộp hai bóng vàng, một quả ở hộp vàng-bạc. Nếu bạn đã rút được một quả bóng vàng, thì bạn có thể đang ở trong ba tình huống: đã lấy một trong hai quả vàng từ hộp toàn vàng (hai khả năng), hoặc lấy quả vàng duy nhất từ hộp vàng-bạc (một khả năng). Như vậy, xác suất bạn đang ở hộp vàng-bạc thực ra chỉ là 1/3, còn 2/3 khả năng là bạn đang ở hộp toàn vàng – nơi quả bóng tiếp theo cũng sẽ là vàng. Vậy xác suất rút bóng bạc tiếp theo chỉ là 33%.
Tại sao trực giác lại lạc lối? Bởi vì nó bỏ qua cấu trúc xác suất ẩn phía sau dữ kiện đã biết. Nó chỉ nhìn bề mặt: có hai hộp hợp lý, mỗi hộp có một khả năng đúng, nên suy ra 50%. Nhưng khi bạn hiểu rõ rằng khả năng lấy ra một quả bóng vàng từ hộp toàn vàng là gấp đôi so với hộp vàng-bạc, thì bạn mới thấy trực giác ban đầu đã đơn giản hóa vấn đề một cách sai lầm.

Trường hợp thứ hai, bài toán "hai con của ông Smith", còn nổi tiếng hơn về khả năng đánh lừa người thông minh. Câu hỏi là: "Ông Smith có hai người con. Một trong hai là con trai. Vậy xác suất cả hai đều là con trai là bao nhiêu?" Và lần nữa, rất nhiều người trả lời 50%, vì họ nghĩ đơn giản rằng nếu một đứa là trai, đứa còn lại có thể là trai hoặc gái – nên mỗi khả năng có 50%.
Nhưng sự thật cũng giống như câu chuyện về ba hộp bóng. Khi bạn liệt kê tất cả các khả năng có thể xảy ra với hai đứa trẻ (giả sử không phân biệt thứ tự sinh), bạn có: trai-trai, trai-gái, gái-trai và gái-gái. Nhưng đề bài đã nói rõ “một trong hai là trai”, nên bạn loại bỏ trường hợp gái-gái. Còn lại ba khả năng hợp lệ. Trong số đó, chỉ có một là cả hai cùng là trai. Vì vậy, xác suất đúng phải là 1/3, tức 33%.
Những ví dụ như thế này không chỉ là trò đùa toán học – chúng cho thấy một thực tế sâu sắc: xác suất không phải là cảm giác. Nó không hoạt động dựa trên "có vẻ công bằng" hay "một nửa là hợp lý". Nó hoạt động dựa trên tập hợp đầy đủ các khả năng, và cách các điều kiện đã biết làm thay đổi phân bố các khả năng đó.
Ngay cả những nhà toán học huyền thoại cũng từng lạc lối trong mê cung của xác suất có điều kiện. Paul Erdős, một trong những tên tuổi lớn nhất của thế kỷ 20, khi được nghe bài toán Monty Hall – một câu đố xác suất kinh điển khác – cũng nhất mực cho rằng "việc mở một cánh cửa không thay đổi gì cả". Dù người đối thoại với ông đã giải thích bằng công thức Bayes, cây quyết định, và dẫn chứng cụ thể, Erdős vẫn không bị thuyết phục. Một người có đầu óc toán học siêu việt, nhưng vẫn có thể bị trực giác dẫn sai đường.
Xác suất có điều kiện không tuân theo logic đơn giản hay công bằng cảm tính. Nó đòi hỏi sự cẩn trọng trong phân tích và một sự cảnh giác nhất định với trực giác. Đôi khi, để hiểu điều gì là “rõ ràng”, ta phải nghi ngờ chính những gì tưởng là hiển nhiên nhất.