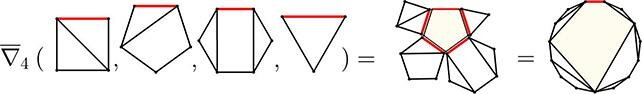Dũng Đỗ
Writer
Một bài toán đại số cơ bản tưởng chừng đã "bó tay" gần 200 năm qua – việc tìm lời giải tường minh cho các phương trình đa thức bậc cao (từ bậc 5 trở lên) – có thể sắp được viết lại. Nhà toán học Norman Wildberger từ Đại học New South Wales (UNSW), Úc, cùng với nhà khoa học máy tính Dean Rubine, vừa công bố một phương pháp hoàn toàn mới dựa trên lý thuyết tổ hợp và số Catalan mở rộng để giải quyết các phương trình phức tạp này, một thành tựu được ông mô tả là "sự sửa đổi mạnh mẽ của một chương cơ bản trong đại số".
Bài toán "bất khả thi" gần 200 năm
Phương trình đa thức là các phương trình chứa biến số với số mũ nguyên không âm (ví dụ x³, x⁵...). Các nhà toán học từ lâu đã tìm ra công thức nghiệm tổng quát cho phương trình bậc 2 (công thức bậc hai quen thuộc), bậc 3 và bậc 4, sử dụng các phép toán cơ bản và phép khai căn (căn bậc hai, căn bậc ba...).
Tuy nhiên, vào đầu thế kỷ 19, các nhà toán học Niels Henrik Abel và Évariste Galois đã chứng minh một cách thuyết phục rằng không tồn tại một công thức nghiệm tổng quát chỉ sử dụng các phép toán cơ bản và căn thức (nghiệm căn - radical solution) cho các phương trình đa thức có bậc từ 5 trở lên. Khám phá này đánh dấu một giới hạn cơ bản của đại số và khiến việc giải các phương trình bậc cao thường phải dựa vào các phương pháp số gần đúng.
Lời giải từ số Catalan và "đếm hình"
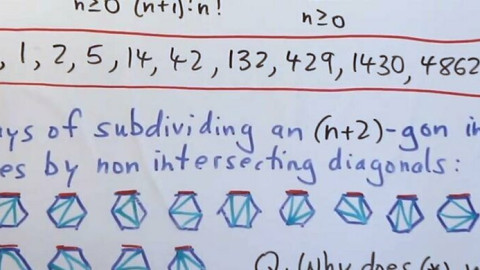
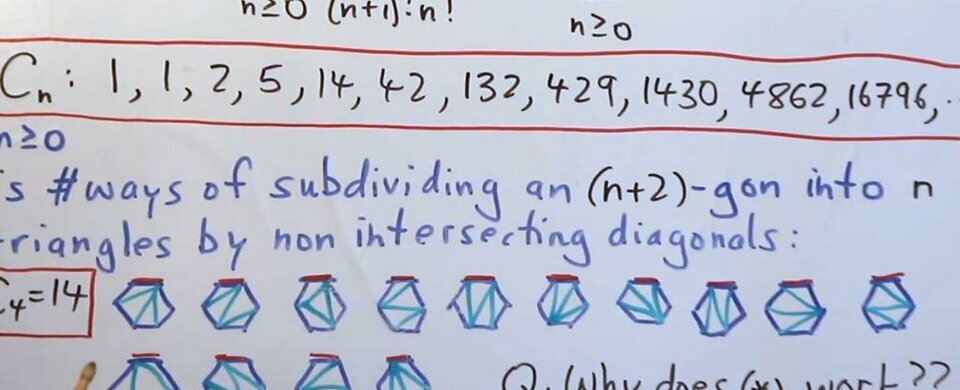
Giáo sư Wildberger và cộng sự đã chọn một hướng tiếp cận hoàn toàn khác, không dựa vào căn thức mà vào lý thuyết tổ hợp (combinatorics) – một nhánh toán học chuyên về các bài toán đếm và sắp xếp. Cụ thể, họ dựa trên số Catalan, một dãy số nổi tiếng trong tổ hợp, thường xuất hiện trong các bài toán đếm cách chia một đa giác thành các hình tam giác.
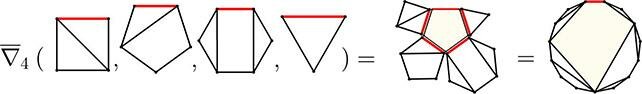
Sự đổi mới cốt lõi của họ nằm ở việc mở rộng khái niệm số Catalan ("tìm kiếm những chất tương tự bậc cao hơn của số Catalan") để áp dụng cho việc đếm cách chia đa giác bằng các hình dạng phức tạp hơn, không chỉ là tam giác. Bằng cách này, họ đã xây dựng được một nền tảng toán học mới, cho phép biểu diễn và tìm ra nghiệm của các phương trình đa thức ở bất kỳ bậc nào thông qua các phép đếm tổ hợp này. Phương pháp đã được kiểm chứng thành công trên các phương trình đa thức lịch sử, bao gồm một phương trình bậc ba nổi tiếng do John Wallis nghiên cứu. Nhóm nghiên cứu còn khám phá ra một cấu trúc toán học mới liên quan gọi là "Geode", có thể là nền tảng cho nhiều phát hiện tương lai.
Tiềm năng ứng dụng rộng rãi
Vì cách tiếp cận này hoàn toàn khác biệt so với các phương pháp đại số truyền thống, nó mở ra tiềm năng "viết lại" và cải thiện các thuật toán cốt lõi trong nhiều lĩnh vực của toán học ứng dụng và khoa học máy tính. Giáo sư Wildberger cho rằng nó có thể ứng dụng vào việc cải tiến thuật toán trong lý thuyết trò chơi, cấu trúc dữ liệu, và thậm chí cả sinh học tính toán (ví dụ: đếm các cách phân tử RNA tự gấp lại).
Nghiên cứu này, được công bố trên tạp chí uy tín The American Mathematical Monthly, không chỉ mang đến một lời giải mới đầy sáng tạo cho một bài toán đại số cổ điển mà còn mở ra những hướng đi mới trong việc kết nối giữa đại số trừu tượng và toán học tổ hợp, hứa hẹn những ứng dụng thực tế trong tương lai.

Bài toán "bất khả thi" gần 200 năm
Phương trình đa thức là các phương trình chứa biến số với số mũ nguyên không âm (ví dụ x³, x⁵...). Các nhà toán học từ lâu đã tìm ra công thức nghiệm tổng quát cho phương trình bậc 2 (công thức bậc hai quen thuộc), bậc 3 và bậc 4, sử dụng các phép toán cơ bản và phép khai căn (căn bậc hai, căn bậc ba...).
Tuy nhiên, vào đầu thế kỷ 19, các nhà toán học Niels Henrik Abel và Évariste Galois đã chứng minh một cách thuyết phục rằng không tồn tại một công thức nghiệm tổng quát chỉ sử dụng các phép toán cơ bản và căn thức (nghiệm căn - radical solution) cho các phương trình đa thức có bậc từ 5 trở lên. Khám phá này đánh dấu một giới hạn cơ bản của đại số và khiến việc giải các phương trình bậc cao thường phải dựa vào các phương pháp số gần đúng.
Lời giải từ số Catalan và "đếm hình"
Giáo sư Wildberger và cộng sự đã chọn một hướng tiếp cận hoàn toàn khác, không dựa vào căn thức mà vào lý thuyết tổ hợp (combinatorics) – một nhánh toán học chuyên về các bài toán đếm và sắp xếp. Cụ thể, họ dựa trên số Catalan, một dãy số nổi tiếng trong tổ hợp, thường xuất hiện trong các bài toán đếm cách chia một đa giác thành các hình tam giác.
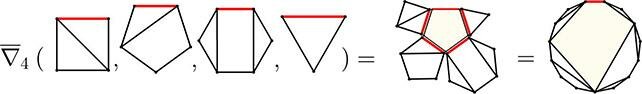
Sự đổi mới cốt lõi của họ nằm ở việc mở rộng khái niệm số Catalan ("tìm kiếm những chất tương tự bậc cao hơn của số Catalan") để áp dụng cho việc đếm cách chia đa giác bằng các hình dạng phức tạp hơn, không chỉ là tam giác. Bằng cách này, họ đã xây dựng được một nền tảng toán học mới, cho phép biểu diễn và tìm ra nghiệm của các phương trình đa thức ở bất kỳ bậc nào thông qua các phép đếm tổ hợp này. Phương pháp đã được kiểm chứng thành công trên các phương trình đa thức lịch sử, bao gồm một phương trình bậc ba nổi tiếng do John Wallis nghiên cứu. Nhóm nghiên cứu còn khám phá ra một cấu trúc toán học mới liên quan gọi là "Geode", có thể là nền tảng cho nhiều phát hiện tương lai.
Tiềm năng ứng dụng rộng rãi
Vì cách tiếp cận này hoàn toàn khác biệt so với các phương pháp đại số truyền thống, nó mở ra tiềm năng "viết lại" và cải thiện các thuật toán cốt lõi trong nhiều lĩnh vực của toán học ứng dụng và khoa học máy tính. Giáo sư Wildberger cho rằng nó có thể ứng dụng vào việc cải tiến thuật toán trong lý thuyết trò chơi, cấu trúc dữ liệu, và thậm chí cả sinh học tính toán (ví dụ: đếm các cách phân tử RNA tự gấp lại).
Nghiên cứu này, được công bố trên tạp chí uy tín The American Mathematical Monthly, không chỉ mang đến một lời giải mới đầy sáng tạo cho một bài toán đại số cổ điển mà còn mở ra những hướng đi mới trong việc kết nối giữa đại số trừu tượng và toán học tổ hợp, hứa hẹn những ứng dụng thực tế trong tương lai.