Homelander The Seven
I will laser every f****** one of you!
4000 năm lịch sử
Hành trình khám phá tỉ số giữa chu vi và đường kính của hình tròn bắt đầu từ hơn 4000 năm trước ở Babylon cổ đại (khoảng 2000 TCN). Với hệ thống số dựa trên bảng đếm và bàn tính, người Babylon dùng 3 làm giá trị gần đúng đủ để tính toán cho các công trình như kho chứa hạt hình trụ. Một tấm bảng đất sét từ những năm 1930 cho thấy họ đã tiến xa hơn, đạt 25/8 (3,125) – một bước nhảy vọt cho thời kỳ chưa có hệ thống chữ viết hiện đại.
Khoảng 1500 TCN, ở Ai Cập, thư ký Ahmes ghi lại trên cuộn papyrus giá trị 256/81 (3,16) nhờ tiến bộ trong phân số. Đến 800 TCN, các học giả Ấn Độ, khi chuẩn hóa xây dựng bàn thờ, đạt 3,138, dù vẫn thường dùng 3 cho tiện lợi. Những nỗ lực này, dù thô sơ, đã đặt nền móng cho các khám phá sau.
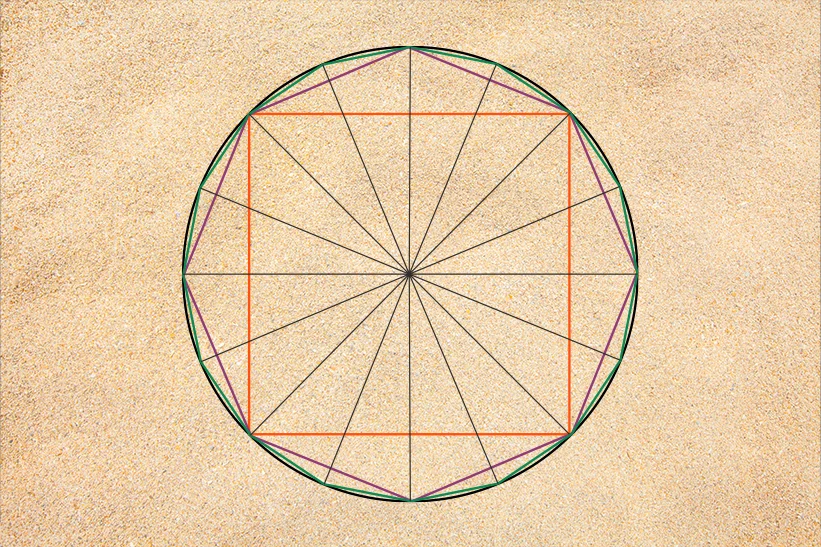
Thế kỷ 3 TCN, Archimedes ở Hy Lạp thay đổi cuộc chơi với phương pháp kiệt sức, dùng đa giác (từ tứ giác đến 96 giác) để kẹp con số này giữa 3 1/7 (3,1429) và 3 10/71 (3,1408). Cùng thời, ở Trung Quốc, Liu Hui áp dụng thuật toán dựa trên đa giác và định lý Pythagoras, đạt 3,1416. Đến thế kỷ 5, Zu Chongzhi đẩy giới hạn lên 3,1415926–3,1415927, một kỷ lục giữ vững hàng thế kỷ.
Những phương pháp tính toán đột phá
Thế kỷ 6, nhà toán học Ấn Độ Aryabhata đưa ra công thức 62832/20000 (3,1416), tận dụng hệ thống số theo vị trí để tăng tốc tính toán. Sang thế kỷ 14, Madhava của Sangamagrama mở ra kỷ nguyên mới với chuỗi vô cực, đạt 3,14159265358 (11 chữ số thập phân) bằng cách cộng trừ các phân số lẻ. Công thức này, sau được gọi là Madhava-Leibniz, trở thành nền tảng cho các tính toán hiện đại.
Năm 1424, nhà toán học Ba Tư Jamshid al-Kashi đạt 16 chữ số thập phân (3,14159265358979323), kết hợp phương pháp kiệt sức với hệ thống số cải tiến. Đến thế kỷ 17, châu Âu bắt kịp với chuỗi vô cực của François Viète và cải tiến từ Christiaan Huygens, James Gregory, và Gottfried Leibniz. Năm 1706, John Machin đạt 100 chữ số bằng cách kết hợp chuỗi Madhava-Leibniz với chuỗi Taylor.
Sự xuất hiện của máy tính vào thế kỷ 20 đã đưa việc tính toán lên tầm cao mới. Công thức của Srinivasa Ramanujan (1910), với chuỗi hội tụ cực nhanh, trở thành nền tảng cho các thuật toán hiện đại. Năm 1988, anh em Chudnovsky dùng công thức này để đạt 1 tỷ chữ số. Đến 6/2024, Jordan Ranous, Kevin O’Brien, và Brian Beeler sử dụng phần mềm y-cruncher của Alexander Lee để tính đến chữ số thứ 202.112.290.000.000 (là 2, nếu bạn nào đang tò mò).
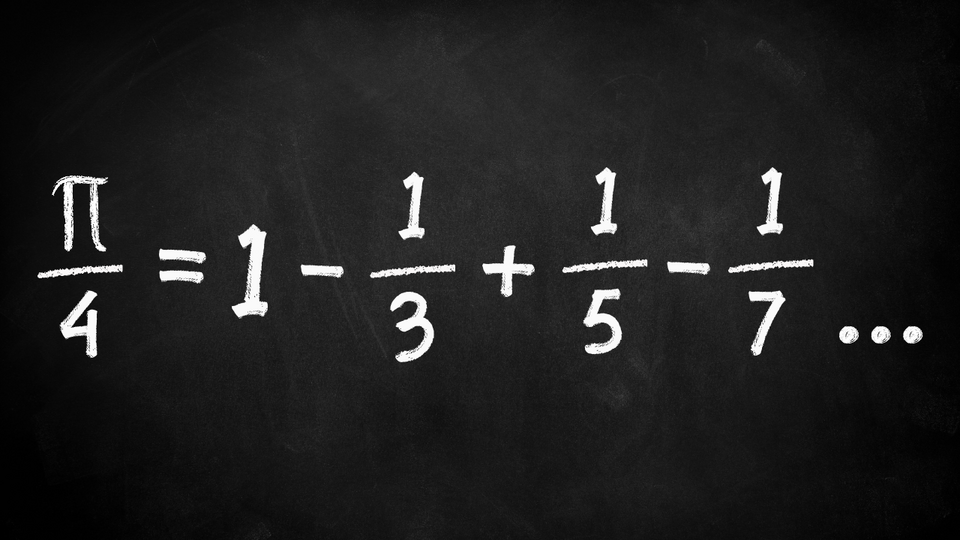
Lý do nhân loại tiếp tục khám phá Pi
Việc tính toán con số này đến 202 nghìn tỷ chữ số vượt xa nhu cầu thực tiễn. Như Marc Rayman (NASA) từng nói, chỉ cần 38 chữ số là đủ để tính chu vi một vòng tròn kích thước vũ trụ với độ chính xác đến nguyên tử hydro. Vậy tại sao nhân loại vẫn không dừng lại?
Trước hết, việc tính toán tỉ số này là bài kiểm tra hoàn hảo cho năng lực tính toán. Các siêu máy tính dùng hằng số để đánh giá hiệu suất phần cứng và phần mềm, như cách y-cruncher đã phá kỷ lục năm 2024. Thứ hai, chuỗi chữ số ngẫu nhiên của nó là bộ tạo số ngẫu nhiên lý tưởng trong khoa học máy tính, hữu ích cho mô phỏng và mã hóa.
Quan trọng hơn, như Simon Clark nhận xét, con số này thể hiện khát vọng hiểu biết của con người. Từ những kho hạt ở Babylon đến siêu máy tính, nó là một thách thức vĩnh cửu, như thể tự nhiên đang nói: “Cứ thử đi!” Việc khám phá thêm chữ số không chỉ là khoa học, mà còn là cách nhân loại khẳng định khả năng vượt qua giới hạn.